Phonetic Matching: A Better Soundex
Alexander
Beider
Stephen P. Morse
This article appeared in the Association of Professional Genealogists Quarterly (March 2010).
Introduction
Researchers are often confronted with the problem of searching for a name in a large imprecise database. The names in the database might be misspelled, or they might not be spelled the way the researcher expected. In either case, looking for an exact match will often result in not finding the name being sought.
Over the years, designers have struggled to develop search applications to cope with this problem. They typically provide an option for finding approximate rather than exact matches. So some criteria needs to be established whereby two names can be said to be approximate matches.
One solution is to say that two names are approximate matches if they sound the same. And a method known as soundex was developed to determine if two names sound alike. A brief history of soundex is given in the next section.
A problem with most soundex-based systems is that they find too many approximate matches, most of which are so far off from the name being sought that they are obviously not useful hits. What is needed is some way to reduce the number of approximate matches by removing the irrelevant ones, while being careful not to inadvertently remove any relevant ones in the process. That is the goal of phonetic matching, and this paper describes how it works and how well it achieves its goal.
The work on phonetic matching was developed jointly by Alexander Beider and Stephen Morse. To simplify the narrative (especially in the case study), this paper is written in the first-person singular as if there were only one author.
The name of the phonetic matching system presented here is Beider-Morse Phonetic Matching, sometimes referred to as BMPM. In this paper it will be referred to as just Phonetic Matching, with the leading letters being in upper case.
Soundex
Soundex is a system whereby values are assigned to names in such a manner that similar-sounding names get the same value. These values are known as soundex encodings. A search application based on soundex will not search for a name directly but rather will search for the soundex encoding. By doing so, it will obtain all names that sound like the name being sought.
Russell Soundex – 1918
The first soundex system was developed and patented by Robert Russell in 1918. Its encodings are generated by assigning digits to individual letters in the name, and using the same digit for closely-related letters (e.g., m and n). Once the sequence of digits reaches a certain length, no additional letters in the name are examined. This restricts the name-matching to only the initial portion of the name.
American Soundex – 1930
In 1930 Russell’s algorithm was modified slightly and used by the Census Bureau to facilitate name searches in the census. This modification became known as American Soundex.
Daitch-Mokotoff Soundex – 1985
The next major enhancement to soundex didn’t occur until half a century later when Randy Daitch and Gary Mokotoff announced their Daitch-Mokotoff Soundex system. This is a soundex system developed for Eastern European names. Unlike its predecessors, it sometimes considers sequences of letters, rather than just single letters, in order to determine how the name might be pronounced. Another improvement is that it sometimes produces more than one encoding for a name, and it considers a match if any of the encodings associated with the name being sought matches any of the encodings associated with a name in the database.
Metaphone – 1990
In 1990 Lawrence Phillips published an article describing a more advanced soundex system that he called Metaphone. Metaphone attempts to produce its encoding based on how a name is pronounced rather than how it is spelled. But it is based on English pronunciation only. Like Daitch-Mokotoff, it too uses sequences of letters rather than just single letters. And unlike all its predecessors, it bases its encodings on the entire name rather than truncating after considering only some initial portion of the name. It didn’t follow Daitch-Mokotoff’s lead of allowing a name to have more than one encoding, but instead generates a single encoding for each name as was done in the earlier systems.
Double Metaphone – 2000
Rather than resting on his laurels, Phillips published yet another metaphone article, this one he called Double Metaphone. The name comes from the fact that it produces two encodings for each name. So it doesn’t have the robustness of Daitch-Mokotoff which can have many encodings, but it is certainly more robust than the earlier systems that have only one encoding per name. Another new feature of double metaphone is that it includes foreign pronunciations, but it lumps all the foreign rules together and doesn’t distinguish which rule corresponds to which language. And Phillips dropped one of the improvements of his earlier Metaphone – namely the encoding is again restricted to the initial part of the name.
Beider-Morse Phonetic Matching – 2008
The Beider-Morse system, described in this paper, attempts to solve a problem inherent in all inexact matching systems to date. Namely the number of matches found is often extremely large and consists of many names that could not be considered relevant by any stretch of the imagination. The Beider-Morse system reduces the number of irrelevant matches by first determining the language from the spelling of the name, and then applying pronunciation rules based on that specific language. It considers the entire name rather than just some initial portion of it. And it provides for multiple encodings.
Irrelevant matches are sometimes referred to as false positives. The next section defines these terms and gives an example.
True and False Positives and Negatives
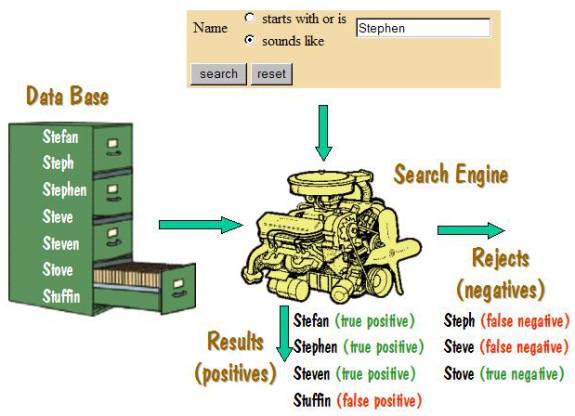
Consider a database that consists of the names Stefan, Steph, Stephen, Steve, Steven, Stove, and Stuffin.
Suppose that we want to search for the name Stephen using some method that will yield precise as well as imprecise matches. Just how imprecise a match we get will depend on the particular method used.
The matches that the search finds are called the positives, and those names that it rejects are called the negatives. Those positives that are relevant are called true positives, and the others are false positives. Whether a match is relevant or not is of course up for debate – it is a judgment call and very subjective. And it has to be subjective – if it were otherwise we could have formal rules for determining relevant matches and the search program could return only those matches that are relevant.
As an example, let us assume that the matches found when searching for Stephen in the above database are Stefan, Stephen, Steven, and Stuffin. The first three are probably relevant, and are names that we would have wanted to see. So these are the true positives. Stuffin, however, is probably not relevant – it is a false positive.
The names that were rejected are Steph, Steve, and Stove. Of those, Stove is probably not one that we would have wanted. So it is a true negative. But Steph and Steve are ones that we would probably be interested in. They are false negatives.
This is illustrated in the following diagram.
Example 1: Washington in the Ellis Island Database
As an example, let’s search for Washington in the Ellis Island database (list of 25 million people who came through Ellis Island from 1892 to 1924). Of course George Washington didn’t come in through Ellis Island, But many other Washingtons did, so it is a good example to study.
If we search for Washington using American soundex, we get over 3,900 unique names. These include names like Wacknocty, Wegonge, and Wozniak. Clearly those are false positives. And, in fact, all but two of the 3,900 names are false positives – the two true positives being Washington and Washincton.
A search using Daitch-Mokotoff soundex gives nine names, six of them being false positives. The true positives include the two found by American soundex, and also includes the name Vasington, Vasington was a false negative under American soundex.
A search using Phonetic Matching gives only four names, but only one of those is a false positive. The other three are the same three true positives found by Daitch-Mokotoff soundex.
The true and false positives for Washington are shown below.

The bottom line is that more than 99% of the positives for Washington under American Soundex are false, 67% under Daitch Mokotoff are false, and only 25% under Phonetic Matching are false.
Example 2: Eisenhower in the Ellis Island Database
Would it surprise you to learn that Dwight and Mamie Eisenhower are in the Ellis Island database? The image of their manifest is shown below.

Of course Eisenhower wasn’t an immigrant. Rather he returned to the US in 1924 after serving as an officer in the Panama Canal Zone, and before beginning his next assignment as an officer in Baltimore. This 1924 arrival is in the Ellis Island database.
If we search for Eisenhower in the Ellis Island database using American soundex, we get 388 unique names, 375 of them being false positives. That means 97% of the positives obtained are false.
Each unique name can appear more than once in the database. We will use numbers in parenthesis to indicate how many times a name appears.
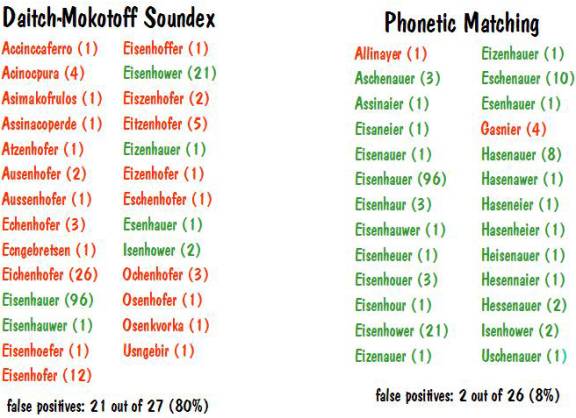
The 13 true positives and the number of times each appears are Eisaneier (1), Eisenauer (1), Eisenhauer (96), Eisenhaur (3), Eisenhauwer (1), Eisenheuer (1), Eisenhouer (3), Eisenhour (1), Eisenhower (21), Eizenhauer (2), Eizenhauer (1), Eschenauer (10), and Esenhauer (1).
If we do the search using Daitch-Mokotoff soundex, we obtain 27 unique names, 21 of which are false positives (80%). And Phonetic Matching gives 26 unique names with only 2 false positives (8%). See the chart below.
Counting matches instead of unique names gives 2421 false positives out of a total of 2553 hits for American soundex (95%), 70 false positives out of a total of 192 hits for Daitch-Mokotoff soundex (37%), and 5 false positives out of a total of 168 hits for Phonetic Matching (3%).
Throwing out the Baby with the Bath Water
Reducing the number of false positives is a good thing, provided we don’t wind up creating some false negatives in the process. In other words, we need to be careful not to throw away the baby with the bathwater. So let’s see if that happened in the case of Eisenhower in the Ellis Island database.
Of all the unique names rejected under American soundex, 11 of them could be considered to be ones we are interested in. Thus they are false negatives. Under Daitch-Mokotoff soundex, 19 of the unique names rejected could be considered false negatives. And under Phonetic Matching, none of the names rejected are ones that we would have wanted. This is shown below.
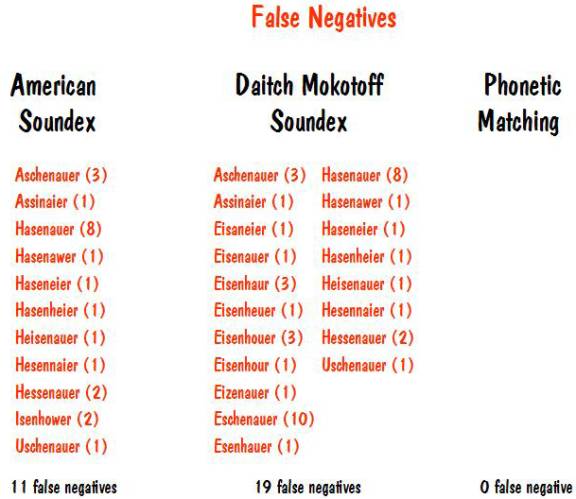
We shouldn’t get too excited over the fact that Phonetic Matching produces no false negatives. This example paints too rosy a picture, and occasionally there will be some false negatives. But hopefully the few false negatives introduced will be more than compensated for by the reduction in false positives.
Example 3: Obama in the Ellis Island Database
Surely Barack Obama won’t be found in the Ellis Island database – he was born 6 years after Ellis Island closed for good, and 37 years after the last entry in the list of 25 million passengers. But that shouldn’t stop us from searching for names that sound like Obama in the database.
Searching for Obama using American soundex gives 781 hits, many of which are false positives. And, of the names rejected, many are false negatives. A search using Daitch-Mokotoff soundex gives 11,584 hits, most of which are false positives. And a search using Phonetic Matching gives just 40 hits, only 2 of which are false positives. The 40 Phonetic Matching hits are shown below.

Overview of Phonetic Matching
OK, that’s enough of a marketing pitch. Hopefully it has convinced you that Phonetic Matching is good. Now let’s see how it works.
Phonetic Matching is based on the principal that pronunciation depends on the language. So the first step is to determine the language from the spelling of the name. Then the name is converted into a sequence of phonetic tokens using pronunciation rules specific to that particular language. And, finally, names are compared based on their phonetic-token sequence.
We have selected a set of languages, and have developed tables for each one. These tables consist of detailed pronunciation rules, as well as rules for determining if a spelling of a name corresponds to the language.
The languages we currently support are Catalan, Czech, Dutch, English, French, German, Greek (in Greek characters as well as translitered into Latin characters), Hebrew, Hungarian, Italian, Polish, Portuguese, Romanian, Russian (in Cyrillic characters as well as various transliterations), Spanish (including its Latin American dialects), and Turkish. New language tables will probably be added in the future.
And for Jewish names we have gone one step further. We have a special variant of Phonetic Matching that is customized for Ashkenazic Jewish names (languages are English, French, German, Hebrew, Hungarian, Polish, Romanian, Russian, and Spanish), and one that is customized for Sephardic Jewish names (languages are Catalan, French, Hebrew, Italian, Portuguese, and Spanish).
Determining the Language
The Phonetic Matching system has about 200 rules that allow it to determine the language that a name is written in, based on the spelling of the name. For example, consider the following two spellings of the same name:
1. Schwarz
The following rules are appropriate in this case:
“sch” at beginning: language is German or transliterated Russian
“rz” at end: language is German or Polish
From these two rules we can conclude that the language is German.
2. Szwarc.
Here we will apply the following rules
“sz”: language is Polish or Hungarian
“c” at end: language is Polish or Romanian
From this we determine that the language is Polish
A Schwarts by any other Name
Here are still more spellings of the same name, and the language corresponding to each:
Schwarz: German
Szwarc: Polish
Schwartz: alternate German
Szwartz: blended Polish German
Şvarţ: Romanian
Svarc: Hungarian
Chvartz: French
Шварц: Russian
שורץ: Hebrew
More Rules for Determining Languages
Some of the language rules enable us
to determine the language uniquely. For example:
“tsch”, final
“mann”, final “witz”: German
Initial or
final “cs” or “zs”: Hungarian
“cz”, “cy”,
initial “rz”, initial “wl”, final “cki”: Polish
Other rules narrow it down to a small
number of languages
final “ck”:
German or English
“sz”: Polish
or Hungarian
And yet other rules eliminate certain
languages
“y”, “k”:
not Romanian
“v”: not
Polish
“kie”: not
French or Spanish
Phonetic Tokens
Once the language is known, we can use
language-specific pronunciation rules to convert the name into a sequence
of phonetic tokens. One possibility for such tokens
is the International Phonetic Alphabet (IPA), where each character in the
alphabet corresponds to a unique sound. The characters
are shown below:
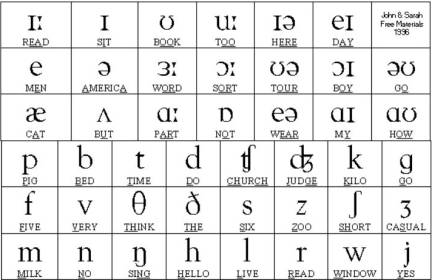
One problem with the IPA set of characters
is that it makes too fine a distinction between similar sounds. Another is that most of the characters are not found on
standard computer keyboards.
For our phonetic tokens we used the characters
in the IPA but simplified it by dropping characters that have similar sounds
to other characters. Where possible, we tried to use
the same character for a sound as is used in the IPA. And
we limited our selection of characters to those found on standard keyboards,
sometimes replacing an IPA character with a standard one that looked similar. For example, we used S instead of ʃ for the “s”
sound in “sure”, and similarly we used Z instead of Ʒ
for the sound of “z” in “azure”.
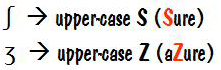
Below is a list of the simplified phonetic
tokens that we selected, along with the sound (in an English word) that each
represents
|
a (part) |
b (boy) |
d (dog) |
e (set) |
f (flag) |
|
g (girl) |
h (hand) |
i (ski) |
j (yes) |
k (king) |
|
l (lamp) |
m (man) |
n (neck) |
o (port) |
p (pot) |
|
r (ring) |
s (star) |
t (tent) |
u (flu) |
v (vase) |
|
w (wax) |
x (loch) |
z (zoo) |
S (Sure) |
Z (aZure) |
Converting Names to Phonetic Tokens
For each of the languages we support,
we have developed a set of rules to convert a name in that language into
a sequence of phonetic tokens. Let’s look at two examples.
1. Schwarz
We have already
determined that this is German. Our set of German
pronunciation rules includes the following:
“sch” => S
“w” => v
“z” => ts
Applying
these rules, we have the following result for Schwarz
“Schwarz”
=> Svarts
2. Szwarc
We already
found that this is Polish. Our Polish rules include
“sz” => S
“w” => v
“c” => ts
So in this
case we get
“Szwarc” => Svarts
Not surprisingly, we get the same set
of tokens in both cases.
Consider the Context
The rules for converting the letters
in a name to a sequence of phonetic tokens need to consider the context in
which the letters are found. Otherwise we could have
nonsense such as the following:
Name: ghoti
“gh” => f (as in enough)
“o” => i (as in women)
“ti” => S (as in motion)
Based on this, we could have the name
ghoti matching the name fish. The problem here is
we didn’t consider the context in which the gh was found.
Specifically the first rule should have been
“gh” => g (if at beginning)
else “gh”
=> g or f or w
Common Rules for Many Languages
There are certain rules that cut across
languages. Two examples of such rules are presented
here. The goal of this is not to make you a linguistic
expert, but rather to have an appreciation that there are such language-independent
rules, and to see how the Phonetic Matching system can take advantage of
them when producing phonetic tokens.
1. Final Devoicing
Final Devoicing
says that at the end of a name (or any word for that matter), voiced consonants
are pronounced like their unvoiced counterparts. Some
examples are:
Lev is pronounced
as if it were Lef
Grand is pronounced
as if it were Grant
Tab is pronounced
as if it were Tap
That’s not
to say that you can’t pronounce Lev with a voiced-v at the end. But it’s just not natural to do so in a number of languages
(e.g., German, Dutch, Polish, Russian), and you would be forcing the issue
if you tried.
2. Regressive Assimilation
Regressive
Assimilation says that consonants acquire the voiced/unvoiced characteristic
of the consonant that immediately follows it. Some
examples are:
Shabse is pronounced
as if it were Shapse
Vitzon is pronounced
as if it were Vidzon
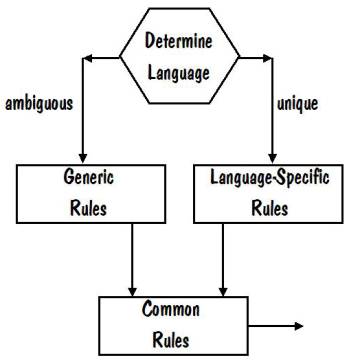
Flow Chart
We are now ready to put the pieces together
and see how a name is transformed into a sequence of phonetic tokens. Note that there is a special set of pronunciation rules
that we apply if we can’t determine the language. These
are called the generic pronunciation rules.
Approximate Rules
We could stop the development of Phonetic
Matching here, and have a perfectly reasonable system. And
indeed some implementers of search applications might choose to do so. But in order to avoid throwing out too many babies with
the bathwater, we added some approximate rules to the system. The use of the approximate rules to reduce the number
of false negatives is totally optional, and at the discretion of the application
developer.
Below are two examples of such approximate
rules.
1. Unstressed Equivalence
This rule
states that unstressed “a” is pronounced the same as “o” and vice versa. So Nixon is pronounced the same as Nixan, and Reagan as
Reagon. However Obama is not the same as Oboma, because
the syllable in which the change was made is the stressed (accentuated) syllable. Simarly, Ford is not pronounced like Fard.
For a number
of languages, this unstressed-equivalence rule is always true. However, it is not trivial to come up with a set of rules
to determine which syllable in a name or word is accentuated. For that reason we will treat “a” and “o” as equivalent
in all cases (stressed or not), and that is what makes the rule “approximately”
true.
2. Phonetic Proximity of a Pair of
Sounds
Certain sounds occurring in proximity are close to (but not exactly the same as) some other sound. For example, “n” before “b” sounds close to “m”. So Grinberg is pronounced approximately the same as Grimberg.
Searching for Matches
There are three steps when searching
for matches in a database. First the names in the
database must be converted to phonetic tokens (encoded). Then
the name being searched for must be converted. And
finally a match is sought between the encodings.
The encoding of the names in the database
is done when the search application is being developed, long before any searches
are done. Since this is not done when the user is
trying to do a search, it doesn’t matter if it takes a long time to do the
encoding, providing we are talking days and not years. The
language of the entire database might be known a priori, in which case it
is not necessary to test each name to determine the language. For example, the names in a Polish telephone directory
could all be assumed to be in Polish. In other cases
the language is not known, such as in the Ellis Island database in which
the languages are all over the map (literally). In
that case, the language of each name would need to be determined on an individual
basis.
The encoding of the name being searched
for is done at the time that the search is done. In
this case, no a priori knowledge of the language is assumed and the language
is determined by the spelling of the name.
Note that a name in the database might
be encoded based on a different language than is used when that name is being
searched for. For example, the name Schwartz in a
Polish telephone directory might be encoded using the Polish pronunciation
rules whereas the name Schwartz being searched for would be encoded with
the German pronunciation rules because Schwartz is a German spelling. In that case, the following surprising (but acceptable)
things might happen:
1. The search might not be transitive
Transitivity means that if A=B and B=C, then A=C. But that is not the case for our searches. Specifically if a search for A finds B and a search for B finds C, then it does not follow that a search for A will find C.
2. The search might not be commutative
Commutivity means that if A=B then B=A. But in our case, if a search for A finds B, it does not follow that a search for B will find A.
Case Study
It would be informative to apply Phonetic
Matching to an actual case and see how it helped provide new information. My paternal grandfather was Louis Mastinsky (Mastinsky
was my father’s “maiden name” which he later changed to Morse). I found Grandpa Louis’s ship record many years ago the
old-fashioned way (using actual microfilm readers), long before the database
was ever put on line. Below is a portion of the manifest
image that I found.

I knew very little about Grandpa Louis. I didn’t know if he had any siblings, and certainly knew
nothing about his more distant relatives such as cousins.
So I was surprised to see that he was going to a cousin, Oswald Mostinsky. But Oswald is listed as living in New Jersey City. There is no such place, so I don’t know if it was supposed
to be New York City, or Jersey City. Oswald lived
on Cannar Street, but I checked and couldn’t find a Cannar street in either
New York or New Jersey. For many years, Oswald was
a dead end.
When the Ellis Island database went online,
I searched it for all names sounding like Mastinsky using Datch-Mokotoff
soundex. I obtained 92 matches. Number
71 was Grandpa Louis. Numbers 55 and 56 were Grandma
Bedanah traveling with Uncle Zelig. And number 22
was Aunt Dora. There were a few people named Mostinski
in the list, and although interesting, I never found a connection to them. All the other names were out in left field (e.g., Mastinicchio)
and obviously false positives that I didn’t want to see.
And since there were so many false positives, I never really looked
carefully enough to see if there might be another true positive lurking among
them.

That’s where my research stood for many
years. When I implemented Phonetic Matching in my
Ellis Island search application, I decided to use Mastinsky as a test case. I obtained only nine hits, as shown below. Among them were Grandpa Louis and Aunt Dora. There were also several Mostinkis and a Mastensky, all
of whom I had investigated and discarded many years earlier.

But now, without a single false positive
on the list, I was able to focus more intently on the names obtained. I noticed a Ju…el Meistinsky, whom I never saw before
because he had been hidden by all the false positives. So
I decided to bring up Ju…el’s record

I could see that what the transcriber
read as Ju…el is in reality Judel. Note that Judel
is going to his brother at 18 Cannon Street in New York City. I checked a map, and indeed there is a Cannon Street in
New York City. Judel (pronounced Yudel) is probably
cousin Oswald. And the brother whom Judel is going
to must be another cousin of grandpa’s. The manifest
is not clear on the brother’s name – perhaps it is Abh. I
immediately checked the 1904-5 Manhattan City Directory for 18 Cannon Street
and found an Abraham Mostinsky living there.
From this I learned that grandpa’s father
had a brother (whose name I don’t know) and that brother had sons Abraham
and Judel. This is information I didn’t know before,
and I found it because I was using Phonetic Matching.
Implementations
There currently exist several implementations
of Phonetic Matching. It is on several databases on
my website (http://stevemorse.org) --
namely the Ellis Island database, the Dachau Concentration Camp Records,
a database of Jewish surnames, and various naturalization databases. Other websites that have implemented Phonetic Matching
are http://sephardicgen.com, https://jewishgen.org, http://jri-poland.org, and http://rtrfoundation.org. In addition, there are several other sites that are currently
considering adding Phonetic Matching to their search applications.
The Authors
Alexander Beider

Alexander Beider (or Sasha as his friends
call him) was born in Moscow in 1963. He received
a PhD in Applied Mathematics from the Moscow Physico-Technical Institute
in 1989. In 1990 he emigrated to France where he received
a second PhD, this one in Jewish Studies from the Sorbonne in 2000.
He has published several etymological
dictionaries of Jewish surnames and given names. He
has also written a number of papers on linguistics, specifically dealing
with the origins and early history of Yiddish.
Stephen Morse

Stephen Morse is the creator of the One-Step Website
for which he has received both the Lifetime Achievement Award and the Outstanding
Contribution Award from the International Association of Jewish Genealogical
Societies, Award of Merit from the National Genealogical Society, first-ever
Excellence Award from the Association of Professional Genealogists Quarterly,
and two awards that he cannot pronounce from Polish genealogical societies.
In his other life Morse is a computer professional with
a PhD in electrical engineering. He has held various research, development,
and teaching positions, authored numerous technical papers, written four textbooks,
and holds four patents. He is best known as the architect of the Intel 8086
(the granddaddy of today's Pentium processor), which sparked the PC revolution
30 years ago.